mnemoにおける普遍的なテク

はじめに

この記事は、TSG Advent Calendar 22日目として書かれました。

タイトルだけ見るとなんかすごい技を紹介するみたいな風に見えますが、そうではなく、普通にやってもらっていて分かりにくいんじゃないかなと思ったりする部分をある程度補完したい、という思いで書こうと思いました（ただ、現状のランキングを見れば明らかにそんなことはなさそうなのでこの記事の意味はあまりなさそう）。

mnemoとは

TSGというサークルが作ったパズル的プログラミングゲームです。mnemo.proでできます。ぜひランキングに登録してください。たのしいです。詳しくは、博多市さんのブログ、パズルゲーム「MNEMO」を製作しましたをみてください。

1を作る

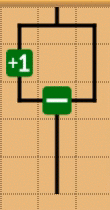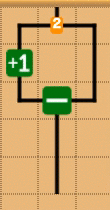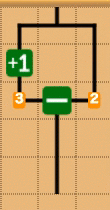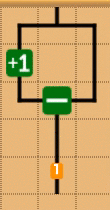
後ろの方では、定数ブロックとして、1が存在しますが、最初の方のステージでは存在しない場合があり、少し詰まるポイントなのかなあと思います。いくつか手法があります。

イコールブロックを使う

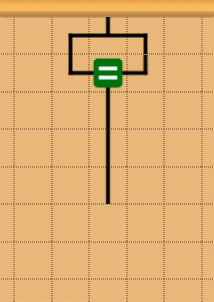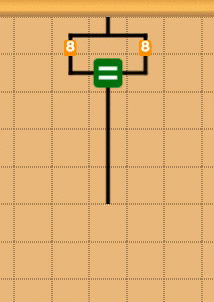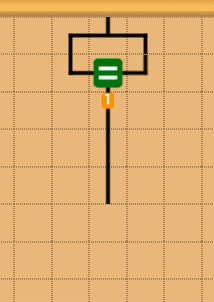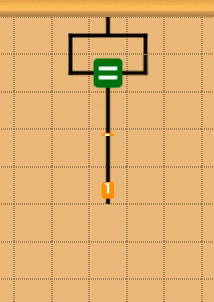
割り算ブロックを使う

これは、入力に0がないことが保証されている必要があります。

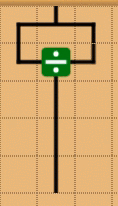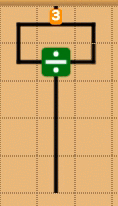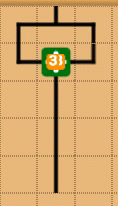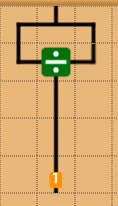
引くブロックを使う

イコールが使えなくて、０が入力にある時（現状あったかわからない）。点数的に弱い

0を作る

まぁ、はい。

余りの計算

mnemoにおいて、流れる数は全て整数で閉じています。割り算についてもその仕様が適用されて、割り切れない場合、小数切り捨てが起こります。切り捨てではないことに注意が必要です。これはC言語と同じ仕様なのですが、をする場合、答えばではなくになります。

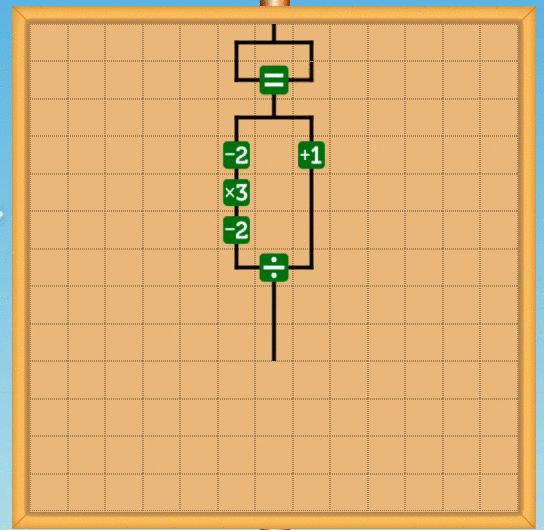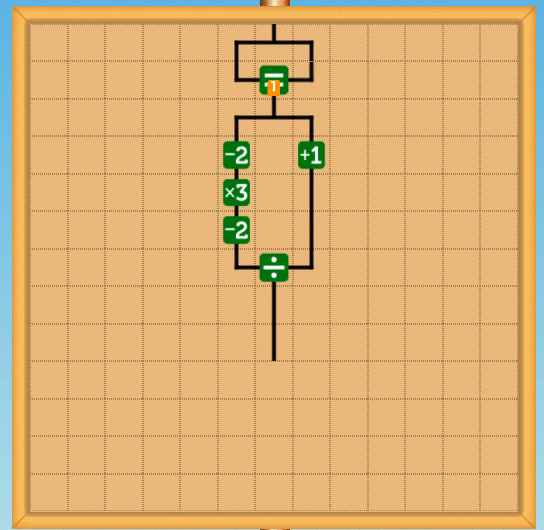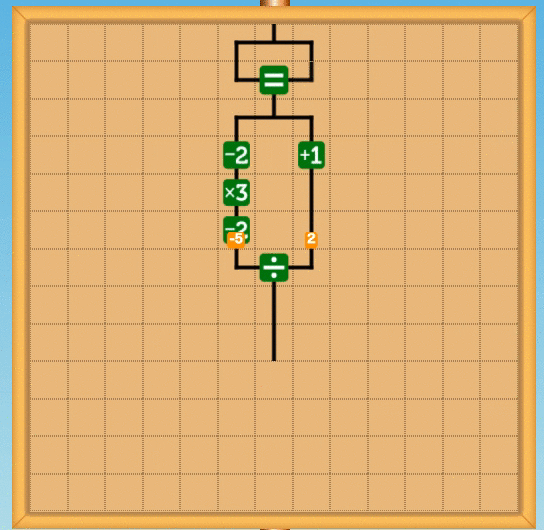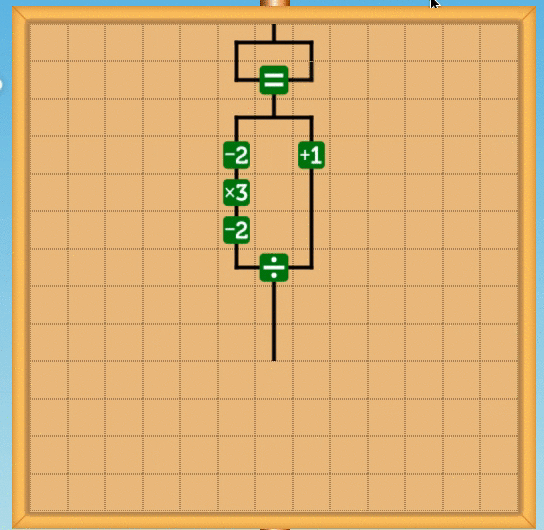
この整数に閉じているという性質を使うと、商を割った値で再びかけ、元の値から引くことで余りが求まります。つまりxをyで割ったあまりrは ということになります。 この場合、負の数では負の余りになりますが、これはC言語でもそうなので、問題はないです（僕は納得いかないんですが。ちなみにPythonは"良い"言語なので、ちゃんと負の数でも正の余りになります）。具体的な回路としては次のような感じです。ここではあまり３を計算する回路を書いています。

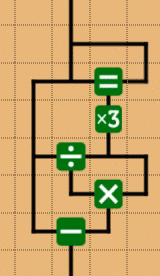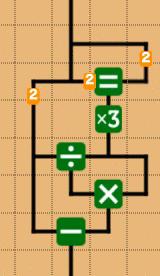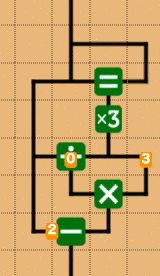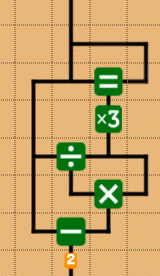
ちなみに、に関しても切り捨てが存在し（mnemoでは、現状、を超えない最大の整数という仕様になっています）、これとをうまく使いこなすことで、うまいことができたりできなかったり・・・？

if then else

トランジスター使うだけですが、なんか思ったより書くことがなかったので。ちなみに、点数を考える場合、トランジスターはやや効率が悪く、できれば、三項演算子を使うべきです（？というやつです）。ここら辺の仕様は、モーダルとしても表示されますが、ここにも、まとめられています。

これも具体的に見た方がわかりやすいと思うので、簡単な回路を書いてみます。実際にあるステージを解いてしまっても面白くないので、ちょっと都合良い設定の問題として「3で割り切れるときは3倍、1あまる時は、2倍、2あまる時は1倍」という恣意的な問題（実際似たようなステージがありますが）を考えてみます。これは愚直に実装する場合、まさに

int f(int x) {
    int m = x % 3;
    if (m == 0) return  x * 3;
    else if(m == 1) return x * 2;
    else return x;
}

という回路を組めばよいことになります。これをmnemoで表現すると、次のようになります。

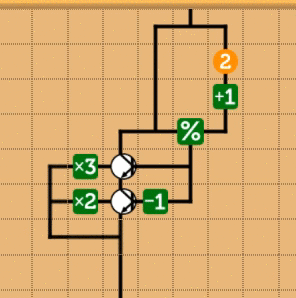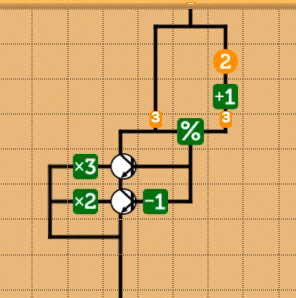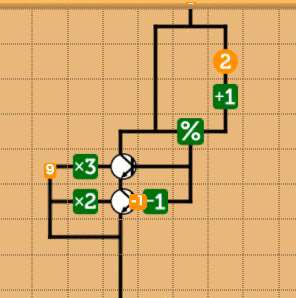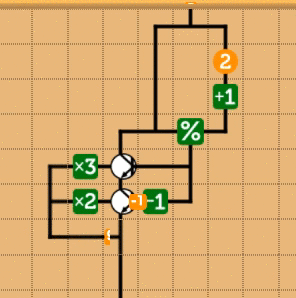
mnemoでは、条件分岐の真偽が0なら偽、0以外なら真となっています。したがって、例えば、1かどうかを判定する場合に、1を引いて0かどうかを判定すればよいことになります。

for

解いている人の数を見ていると、ループ問を解いている人は少ないです（時間がかかるからという理由が強そうですが）。再帰などを含まない回路の場合、ループカウンタを使ったループは非常に簡単にかけます（なので解いて・・・）。これは見た方が早いので、具体的な回路を組んでみます。10という数が上から流れてきて、1~10を（愚直に）足しあげるという操作を考えると、次のようになります。ちなみに、これを少し書き換えるだけで、階乗ステージはクリアすることが可能です。

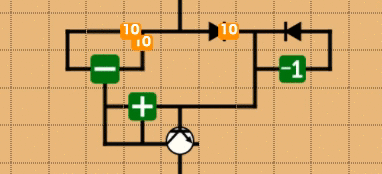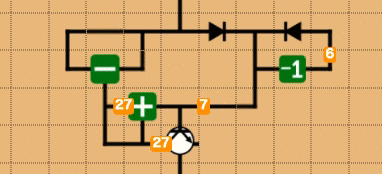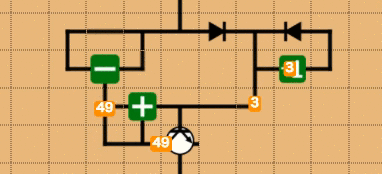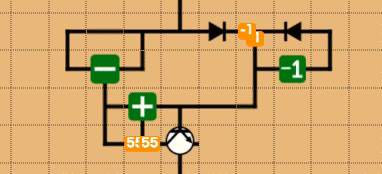
点数の原理

mnemoの点数計算は、hakatashiさんによって生成されたとある式によって計算されています。定義が、一応、wikiにある案１というものになっています。簡単に言えばクロックが少なく、使ったブロックが少ない方がよいスコアになるようになっているはずです。ただ、ブロックは条件分岐が3点、演算子系が2点の重み付けがされているので注意が必要です。

さいごに

@hakatashi is pro.